Hey my friend, welcome back! Today we’re going have a special talk.

Hello V, what’s that? Is this another coffee break?

Hm… not exactly.

It’s about a new ambigram type. Not just a new type, a whole new category!

Wait, what? Really? Does the title “filter” have to do something with it?

Yes. I’m not sure of the best way to introduce it. I think I’ll just share it and get the conversation rolling. Are you ready?

Of course!

Great! Here’s a piece from Otto Kronstedt. It’s called “Hide in plain sight”.

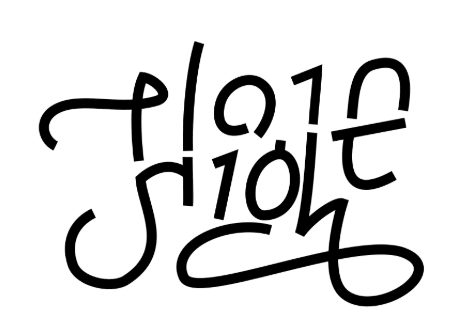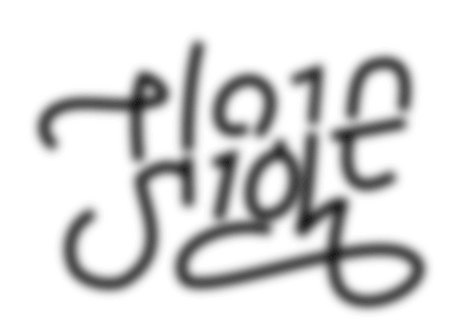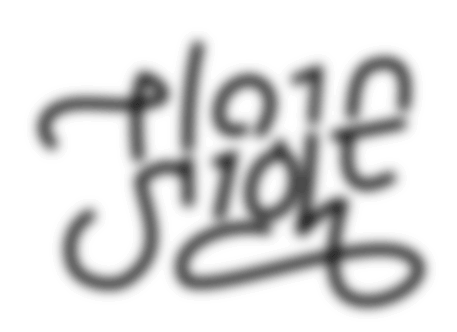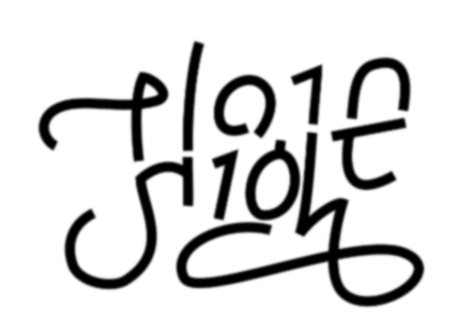
Can you see what happens here?

I read ‘plain sight’ when it’s in focus and then I read ‘hide’ when it gets blurry.

That’s right. But let me ask you something. Do you think that this piece belongs to the mind category or the geometric category?

Hm… I would probably say ‘mind category’. But also, a transformation there, so does it belong to the geometric category as well? Can that be the case?

You’re right that there is a transformation there. We have the first image, then it gets blurry and we get the final image. As for the category, let’s remember the core function of an ambigram first, and test both options.

The core function of an ambigram is this:

• I read something
• Something happens
• I can read it again

If “something happens” to the art, we have a geometric ambigram.
If “something happens” to the viewer’s mind, we have a mind ambigram.

Let’s start by assuming that Otto’s piece belongs to the mind category. What would that mean? It would mean that “something happens” to our mind, the viewer’s mind. But that’s not the case here. We obviously see a transformation. This image gets blurry. Mind ambigrams are still images. Motionless art, with no transformations. Mind ambigrams require the viewer to change their perception and read something else by just looking at a still piece of typography. Otto’s piece displays an animation from the focused image to the blurry one. It’s not motionless. What happens here is not just in the viewer’s mind, it happens to the art. So, it cannot be the case that ‘hide in plain sight’ is a mind ambigram.

It must be a geometric ambigram, right? Well, let’s test this assumption as well. Do you remember what categories of geometric transformation there are? We talked about it here. There are rigid transformations and non-rigid ones. There are three rigid transformations: rotation, reflection, translation, and they preserve the original shape, size, angles, dimensions of an object. On the other hand, non-rigid transformations alter those qualities. Such transformations are: bend, twist, shear etc. Here’s an example for the visual learners.

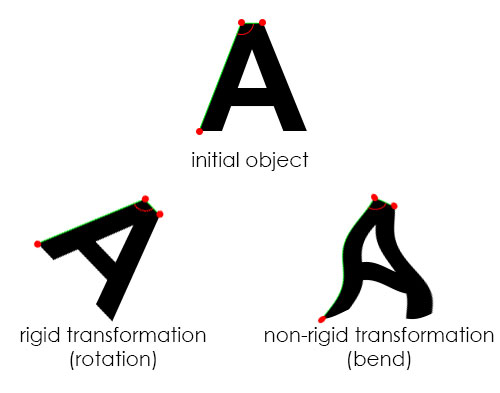
In every geometric transformation, you can always map the vertices (red) and edges (green) of an initial object to the transformed version of it. Also, you can clearly say if a specific point is inside the shape (it will be black) or outside (white).

But let’s see what a blur is.

In the blurred image, you cannot map exactly vertices from the initial object. Nor can you exactly map the edges. And you cannot say for sure if a specific point is inside or outside the shape. It’s not just black and white, it’s gray! If you point at somewhere, it will probably be gray, let’s say 30%. What’s that? Did we point at an edge? Did we point inside or outside the inital object? We’re not sure. If that was indeed a geometric transformation, we would be able to answer all of that.

So clearly, blur is not a geometric transformation either. Which means that “what happens” in Otto’s piece does not happen to the art itself. That’s leads us to think…

If the transformation does not happen to the art itself, nor to the viewer’s mind, where does it happen?

And the answer is simple…

In between!

In between?

That’s right my friend, in between. The artist created his piece and in order to achieve duality, he cleverly placed something in between you, the viewer and the art. He added a…

   Filter 

So, is filter a new category?

Absolutely! And here’s the the explanation of the ambigram categories again.

The core function of an ambigram is: • I read something • Something happens • I can read it again

If “something happens” to the art, we have a geometric ambigram.
If “something happens” to the viewer’s mind, we have a mind ambigram.
If “something happens” in between those two, we have a filter ambigram.

That’s amazing! So, we can create duality by adding things in between us and the art?

Oh yeah! But for a moment, let’s admire the new category we just discovered.

Ok, this may seem small. But hey! We have a new group in town! Let’s celebrate that! And for all of this, thanks to Otto Kronstedt. Thanks man!

That was indeed a genius piece from Otto.

But now… there are a lot of questions that need answers. Is blur the only thing that we can have in between art and the viewer? What even is a filter? What about the hierarchy we talked about last time? How can a filter create duality? What’s the best way to explore this new horizon?

Let me ask you a simpler question Vassilis. Why did you choose pink? Shouldn’t teal be in-between?

Hahaha! That’s a great question. Any colour could literally be used for all categories, since our goal is to make a distinction between those.

But that aside, I chose green for mind ambigrams since green often symbolizes growth, creativity, harmony. It’s the base colour. It’s the grass on which we all stand. It’s the ground.

I chose blue for the geometric ambigrams since blue in design conveys stability, logic, precision, and structure. Just like geometry. Also, it’s like the sky that turns around or the sea that reflects things.

But filter?… I find pink suitable because it’s a bright colour, it’s in the opposite side of the green-blue part of colour spectrum and it’s something that disrupts this colour harmony. It’s rare. It’s like we are putting our cool magic glasses on and discovering new realities in our world.

Oh, I see… so now, how do we explore this new horizon?

Well, for a moment let’s clarify what I mean when “something happens” between the art and the viewer’s mind.

Imagine that you visit an art gallery. An ambigram gallery. You get your ticket and you pass the green entrance. The first hall displays mind ambigrams. Still posters. Motionless. You see two or more readings in each piece. You’re in awe. How awesome are the artists?!

Next hall, blue entrance. Geometric ambigrams here. The things are getting more interesting. There is motion. Gears that rotate posters on the wall featuring rotational ambigrams, vinyl stickers on glasses that feature mirror ambigrams that you can read from the other side, complex gear mechanisms that display jumblegrams. Wow! That’s amazing!

Next door, that’s a pink door. What could possibly happen here? Here’s what you see. A motionless typography piece on the wall. Just like before. It reads ‘plain sight’. But there is something more. There is a blurry glass in front of it. You walk. The path leads you to stand right in front of that glass. And you see this.

Wow!

It will be a unique experience. The art installation is not just a flat piece of canvas. It includes the surroundings, a blurry piece of glass, that when it gets in between you and the canvas, allows you to read a second word. That’s the ingenuity of this piece.

So, do filter ambigram have to do with the third dimension?

It’s not necessary. The original image by Otto was a 2d animation that we all viewed through our screens. But either way, it’s clear that something got in between you and the art piece that lead you read something else, in a way that neither a geometric ambigram nor a mind ambigram could do.

Clever!

Indeed! Now, that we scratched the surface, it’s time to explore this territory, my friend. Shall we?

You have to ask? Let’s jump into it!

Did you like Otto’s piece? Did you expect that there would be a third horizon?

Send me your comments at [email protected].