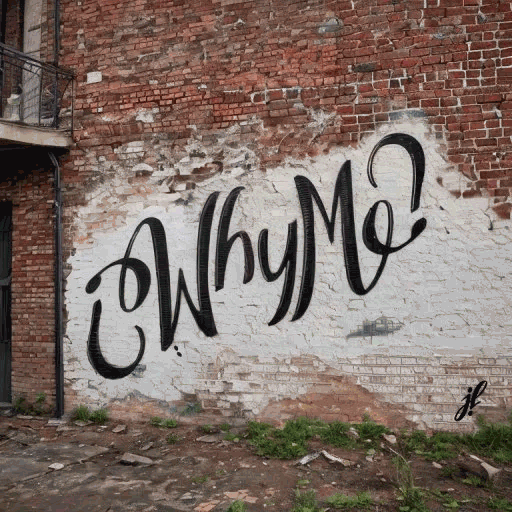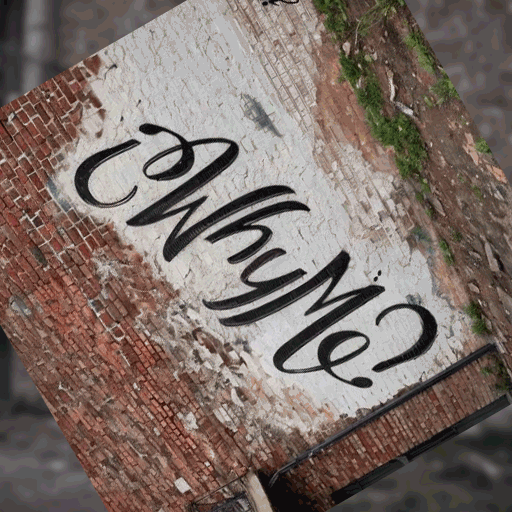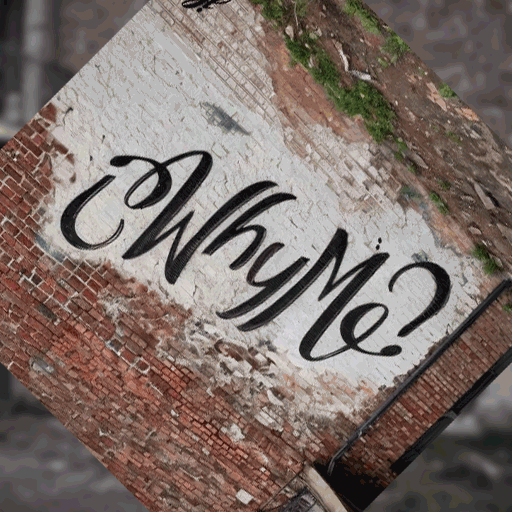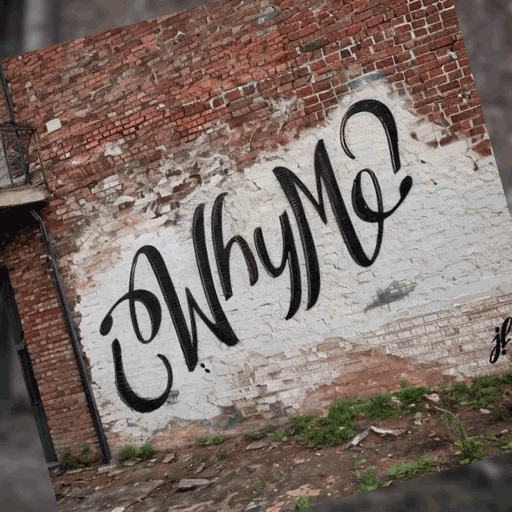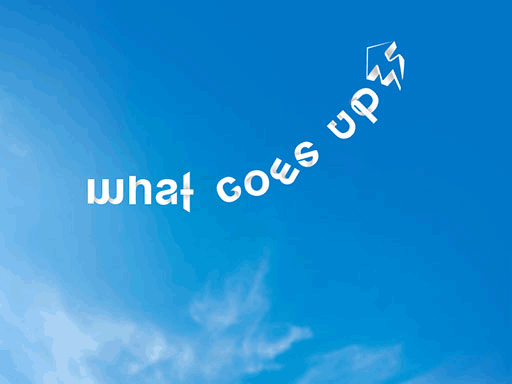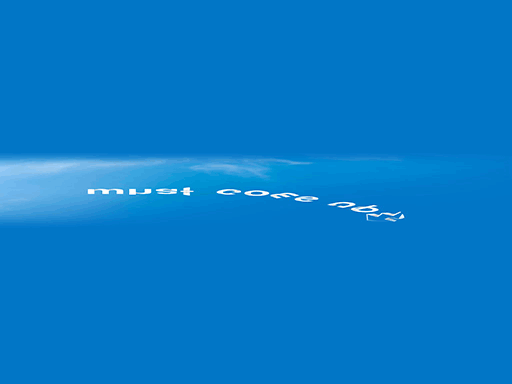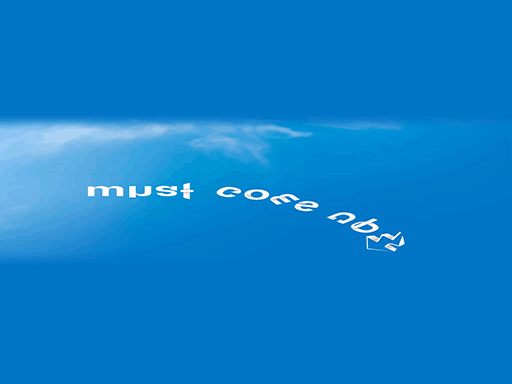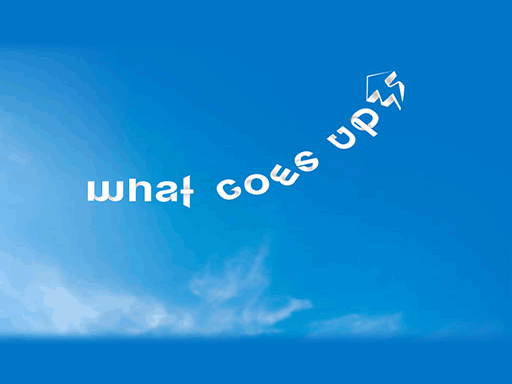What geometric transformations are there?   

 

Geometry features two general categories of transformations, rigid and non-rigid.

 

I’m not going to give a mathematical speech here, so I’m going to use single words. There are three rigid transformations out there and these are: rotation, reflection and translation. Rigid means that after any of those transformations, the shape will still have the same size, area, angles and line lengths.

 

If you cut a piece of paper, for example, let’s say a triangle, and you leave it on the table, then rotate it, then move it, then flip it, it will always have the same shape, same size etc. Pretty natural. It’s not that you stretched it, right?

 

Right.

 

Now imagine that this triangle is made out of rubber. You can stretch it. You can bend it. You can twist it. These transformations are non-rigid. Simple, right? I’m sure you’re smart enough to get it.

 

Ooooh yes! I get it.

 

Well… ok?… I want to leave the non-rigid transformations for the future and take a deep look on the rigid ones, the popular ones. And what’s more popular than…

 

   Rotational ambigrams   

 

It’s when you rotate something.

 

You gotta be kiddin’!

 

When the whole word rotates, you have a rotational ambigram.

 

Here’s an example. It’s “wave” by Vassilis Stergioudis. This one rotates 180°.

 

 

Wait! Why do you refer to yourself as in a third person?

 

That’s the policy of the author of this site. Here is another one. It’s “Why me?” by Jennifer Lynch, aka Imriaylde.

 

 

And another one. It’s “stradivarius” by HC Laborie, aka Haschone.

 

 

Did you know that you can have other angles than 180° as well? Here is another one that rotates 90°. It’s “zen” by Diego Colombo.

 

 

Oh cool!

 

Yes, and here is an interesting one that features a 120° rotation. It’s “sun” by Otto Kronstedt.

 

 

 

Oh, rarely you see a 120° one!

 

I agree. It’s harder to draw a letter being legible in three orientations than in two.

 

Rotational ambigrams are the most common type of ambigrams we see these days. They have subtypes, 180° ambigrams, 120° ambigrams, 90° ambigrams and so on.

 

Cool! What’s next?

   Reflective ambigrams   

 

It’s when you reflect something. Note that I didn’t say “mirror”, and I will explain why in a moment.

 

When the whole word reflects about an axis, you have a reflective ambigram.

 

Here’s an example. It’s “Got milk?” by Bryan Sanders.

 

 

This one had a vertical axis in which the art reflects. Here is another one. It’s “yellow orange” by James Gowan.

 

 

Now here is another one that has a horizontal axis of reflection instead. It’s “what goes up must come down” by Murilo Silva Tanajura, aka Mugga.

 

 

I’ve seen such pieces. This is a lake ambigram.

 

Yes, here is another one. It’s “space-time”, by Otto Kronstedt.

 

 

And now, here is a magnificent piece that features a 45° axis of reflection. It’s “white” by Mugga as well. What would you call that?

 

 

 

Wooo…. what? what’s this? 

 

We will find out in a moment. Here is another one, using the same principle of 45° axis of reflection. It’s “BOOM” by Nopke.

 

 

These are definitely not a lake… nor a mirror…

 

Yes, all of the above are reflective ambigrams. As in rotational ambigrams, reflective ambigrams have many sub-types as well. In fact, we, artists, have given names to some of these sub-types, as you mentioned! Does the piece have a vertical axis? Here you are, a mirror ambigram. Just like the reflection in a mirror on your wall. Does the piece have a horizontal axis? Lake ambigram. Just like the reflection on a lake. Diagonal axis? No idea.

 

We should come up with a name for this!

 

You are right. What physical object reflects diagonally?

 

Hm… A diamond?

 

I like that! Also, diamonds can reflect in all angles, not just at 45° as the example above. So we covered every angle possible.

 

So we have mirror ambigrams, lake ambigrams and diamond ambigrams?

 

That’s right.

 

Another popular sub-type of mirror (this is sub-sub-type of reflective ambigrams) is “totem”, where there is a vertical axis of reflection and the word reads vertically instead of horizontally. Here’s a totem. It’s “The Da Vinci code” by John Langdon.

 

 

I’ve seen such pieces. These pieces can work with letters that are symmetrical or almost symmetrical in the vertical axis, such as T, O, E and M. Hey, V, did you know that you can design a totem reading “TOTEM”?

 

Oh, no, I didn’t. Thanks for the tip, my fellow reading pal!

 

Now let’s move on to…

   Translation ambigrams   

 

It’s when you move something.

 

Wait, is that a thing? Why is this a geometric transformation? You just moved something, but it stays the same.

 

Well, follow me for a second. Put an ambigram on the table. Now stand up. Now step back. Now go to the other side of the table. Did something happen to the art itself? No. Did you see it from a different perspective when you stepped back and when you got to the other side? Yes. You moved, the projection changed. You rotated around the table, the projection changed again. Got it now? Well, in our study, the spectator stays still and the art gets rotated, reflected or translated.

 

So does this mean that, if I write something on a piece of paper, read it, then move it and read it again, is this an ambigram? What are you talking about? This is just silly.

 

No, my friend. We shall change our perception on what a translation on an ambigram art piece really is.

 

Think of pacman for a moment. When he gets to the right side of the screen, he appears on the left. Isn’t he always moving right?

 

Yes.

 

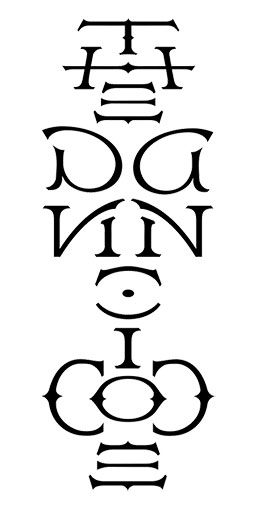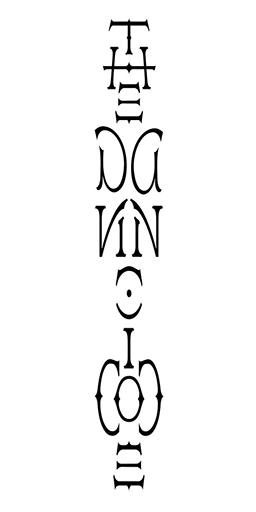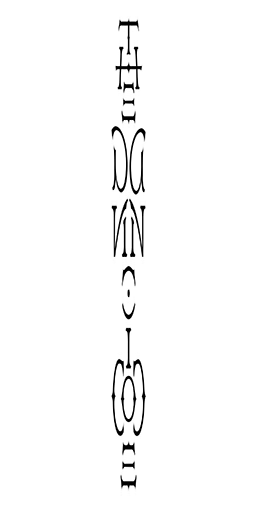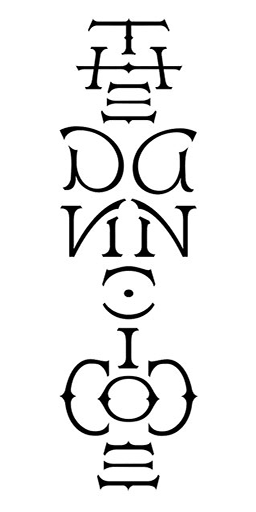
Now think of the screen being your art. Your ambigram. The canvas is not infinite. It’s the screen. When you move the ambigram to the right, the most-right letter disappears and reappears slowly from the left. This is a translation ambigram. Here’s a translation ambigram by Vassilis. It’s “paces into space”.

 

 

Wo, wo, wooooah!

 

Yey, yey, incredible, right? Here’s a polished version of that one.

 

 

Oooohhh…

 

Here’s something more interesting! You can also move the word to the top and have it reappear from the bottom. In this case, I’ve not designed a full word, but a single letter. The D can turn into a K.

 

 

 

Wha.. oh… dk… Idk… what?

 

Well, D and K are just a pair of letters that works naturally in this case, but you get the meaning. You can not only slide letters right and left, but also up and down. Isn’t that amazing?

 

I mean… my mind is blown. I’ve never thought of that!

 

Me neither. At least before I did this study. When I discovered this, my mind was blown too! And now we both know it. Everyone knows it. Now go out there and draw some translation ambigrams, my friend!

 

I’ll give it a try! But, can we just change that name? I don’t like translation ambigrams as a name. It’s too… scientific.

 

Well, why not? I’ve already thought of that and I came up with “slidegram”.

 

Ooooh, I like that! Slidegrams it is then! So, what are these two sub-types of slidegrams called?

 

I guess the “paces into space” ambigram is a horizontal slidegram. The D-K is a vertical slidegram. Actually, you can also have a diagonal slidegram.

 

What? Really? How would that work?

 

The word would slide both left-right and top-bottom, at a specific angle and distance.

 

Tricky! Have you ever done one?

 

Not yet, but the theory is there. I’m sure someone will try creating a diagonal slidegram soon! If not, we’ll work together and create one in the future, what do you say?

 

I would love to do so! So, can you sum up what we currently know about geometric ambigrams?

 

Of course, here’s the map of the blue horizon, that’s how I like to call it.

 

 

Nice! Now what?

 

Well, you tell me. What do you think comes next?

 

I don’t know. We maybe should move to the mind category.

 

No, no, not yet!

 

Why’s that? All rigid geometric transformations achieved. Aha! I got it! Non-rigid transformations?

 

No, not yet.

 

Well, as said, all geometric transformation unlocked. Mission complete. Let’s move on to the mind ambigrams, I’d say.

 

Stay with me. There is more in this blue horizon, I promise. And this is because… there are the…

CUT!

 

Director: CUT!

V: What are you doing?

D: You gave a promise, Vassilis.

V: Oh… oh… I remember. So, what do we do now?

D: We’ve let them know that there is a newsletter form right down below, so they will be informed when the next chapter is released.

V: I like it. What if they don’t?

D: No problem, they’ll come after a while and check. It’s optional.

V: I like it more. Here’s the form my friend!