Where were we when we left, my friend?

 

You said there’s more on this blue horizon, V.

 

Of course there! Here, let’s take a look at the blue horizon map as it currently stands.

 

 

And now, let’s take a look at…

   4-way ambigrams   

 

What is a 4-way ambigram?

 

Well, it’s when you have more than one geometric transformation, while each one displaying a different word.

 

Here’s a 4-way ambigram by Otto Kronstedt reading “mind-soul-heart-body”.

 

 

You see the transformations? First, it reflects. Then, it rotates. Then it reflects again. And it rotates one more time to come back to the starting position.

 

That’s nice!

 

I agree with you. I find this type really cool and hard to draw, so here’s another piece by the same artist, called “serenity-courage-wisdom-gratitude”.

 

 

Oh my!

 

I am in awe as well. How do people even think of that?

 

Here’s something else. If a 4-way ambigram is too difficult to imagine, you can always go for a 3-way ambigram. A 3-way ambigram uses three geometric transformations instead of four. Here’s an example by Otto again, with title “good-bad-ugly”, using a mirror reflection, a diamond reflection and a 90° rotation.

 

 

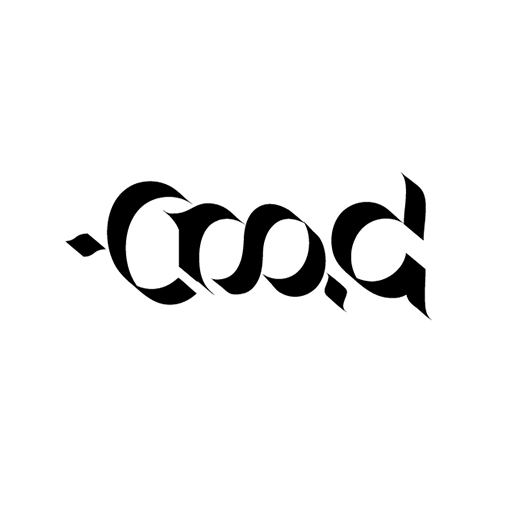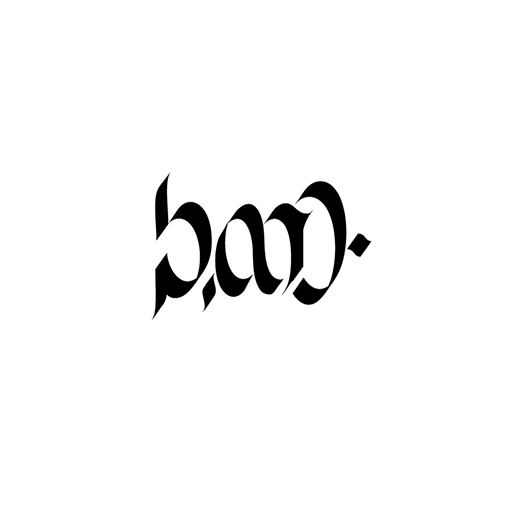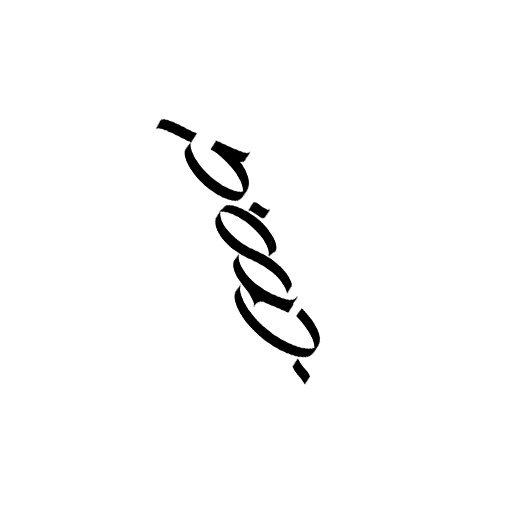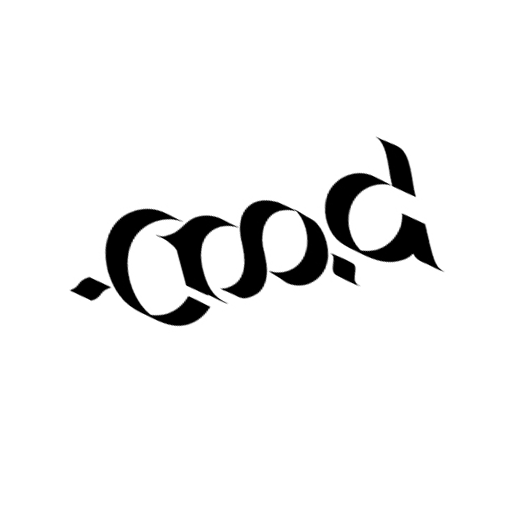
Technically speaking, a 4-way ambigram is not an ambigram. It’s a tetragram. You cannot have 4 ways of reading something that by definition is “read in 2 ways”. The same happens with 3-way ambigrams, they are technically trigrams. But I strongly believe they have a place among ambigrams. So who cares? Rule No 4: Break the rules. This is art. Let all of these be ambigrams!

 

Now let’s see the ambigram map again. Where should we put 4-way ambigrams?

 

 

These ambigrams fall right under all of the previous types, since they share the transformations above them. You could argue that there are the rotational-reflective ambigrams, or the rotational-translating ones, or the reflection-translating ones. I would argue that they also include non-rigid geometric transformations. But here comes rule no 3, keep it simple, remember Einstein’s quote? The core meaning of this type is “the ambigram that has more than one geometric transformation”. This is simple enough.

 

I agree.

 

As for the name of this type, I’m not sure if 4-way or 3-way ambigram is the ideal choice.

 

So, what are we going to call them?

 

That’s a good question, let’s think… an RRT ambigram is awful (R from rotation, R from reflection, T from translation). MTOGT (more than one geometric transformation) is even worse! Oh my God! This is hard. Let’s try one more. Hmmm… a thoroughgoing ambigram? Ugh…

 

There must be a simple name that describes these ambigrams. After all, they just use multiple transformations.

 

That’s it! Multiple. That’s the word! Thanks my friend! We’re going to call them multigrams.

 

Multigrams, I like that!

 

Plus, it removes the need to show what transformations and how many of them are there. Hooray! Here’s the map again.

 

 

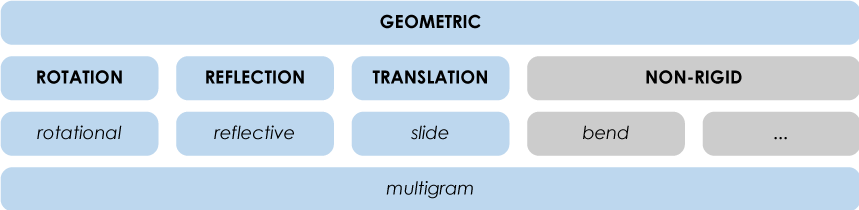
I like how it’s going.

 

I like it too. The areas we haven’t yet explored are still gray.

 

I guessed that.

 

So, should we move on to mind ambigrams, my friend?

 

Well, I think so. Then the table will be complete. All transformations achieved. By themselves or combined. What else should be there?

 

This was a trick question my friend. Do you want to leave this awesome blue horizon so early?

 

What do you mean early V? It’s all there. Plus, there’s no place in this table to add a cell. Do you mean there’s more than that?

 

What if I told you we weren’t even halfway though this table?

 

Not even half-way? Impossible…

CUT!

 

Director: Do you think there’s more than that? Drop a message into [email protected] and subscribe to the newsletter to be the first to find out what comes next.