Jumblegrams
Jumblegrams 
What are juglebr… jugrebl… jugglebram… what are these anyway?
My friend, I know you are a little confused, so are jumblegrams! Confused ambigrams! Take a look at this one, it’s “supply/demand” by Otto Kronstedt.
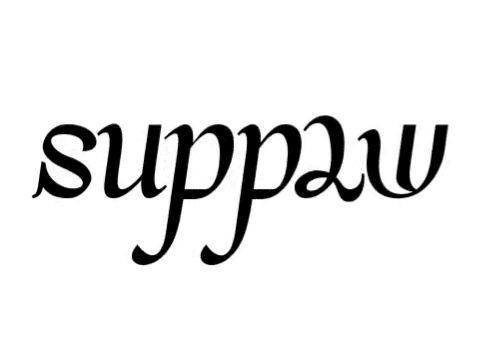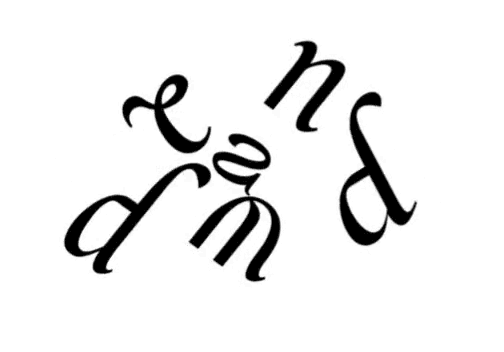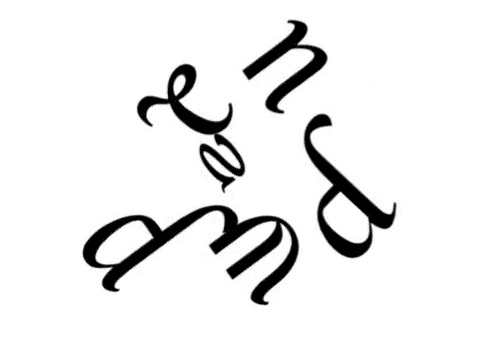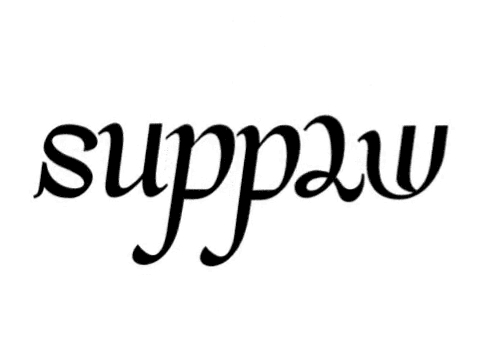
Wow, what’s happening here?
In a jumblegram, every letter rotates, reflects and moves to another place within the word in order to be read as a different letter. See the translation (slide) here? Some letters not only rotate or reflect, they also move.
Can you explain what happens in this image more clearly?
Of course. Starting from left to right, the ‘s’ reflects and becomes an ‘a’. The ‘u’ rotates and becomes an ‘n’. The two ‘p’s also rotate and become ‘d’s. ‘L’ and ‘y’ similarly rotate and become ‘e’ and ‘m’ respectively. Last, all letters move to another place within the word.
So ‘u’ reflects and translates and all the other letters rotate and translate.
That’s right! They jumble. Hence the name.
Can you show me another example?
Here’s “butterfly-caterpillar” by pTshark.

Since there are many translations, rotations and reflections here, the artist has provided a guide to what’s happening.

Some letters move and rotate such as ‘p’ turning into a ‘b’, some others move and reflect such as ‘r’ turning into an ‘f’, while the first ‘r’ of caterpillar just slides!
Now let’s see the ambigram map again and see where we can put jumblegrams.
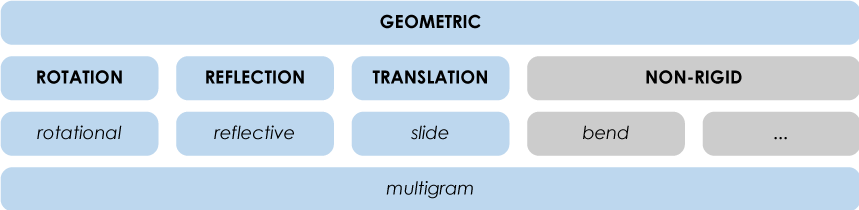
It seems to me that a jumblegram uses multiple geometric transformations. Shouldn’t it be the same as multigrams?
At first glance, you could say yes. But I will explain just how multigrams and jumblegrams are different.
In a multigram, the whole word first rotates, then reflects, then rotates again and so on. In a jumblegram, every letter either rotates, or reflects, or translates or does some combination of geometric transformations.
Which is to say, there is difference to where the transformation happens. In a multigram, the word as a whole goes through a series of geometric transformations, while in a jumblegram, the glyphs transform individually.
So, jumblegrams fit just below multigrams, creating two distinct groups. The first group has all the ambigrams we talked about earlier, where the transformation happens in the whole word, while the second group is where the transformation happens to each glyph separately.
I will name these two groups: “whole word” and “each glyph”.
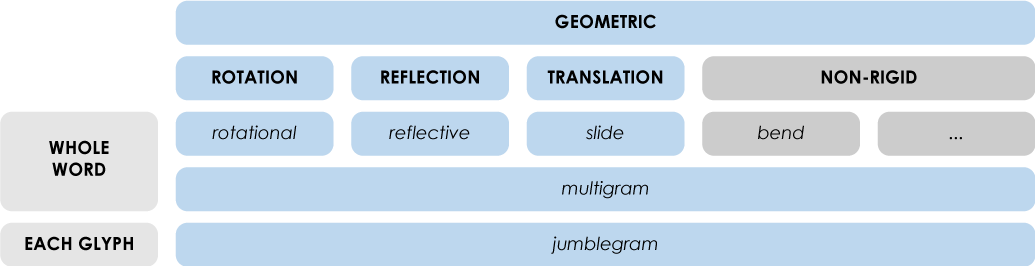
And now I’m thinking… is this the end of geometric ambigrams?
Well… yes?
Look at the table once again. What do you see?
Five types of geometric ambigrams.
What else? Can you see it?
Well… no?
Follow my thoughts here, my friend…