Hello my friend, let’s see where we’re left in the geometric ambigrams map.

 

 

Do you see what I see?

 

Well… no?

 

Follow my thoughts here. If the ‘whole word’ group has two rows, the first one including ambigrams that have only one geometric transformation, and the second one having more than one, shouldn’t it be the case that the same happens in the ‘each glyph’ group? Shouldn’t we have ambigrams that have only rotation, or only reflection, or only translation to each glyph separately?

 

 

 

Oh, I see…

 

Taking advantage of the jumblegram naming, I will name these types: rotatogram, reflectogram, slidogram and so on. I will leave them gray until we find out how they look like.

 

   Rotatograms   

 

So, how does a rotatogram look like?

 

A rotatogram has the rotation happening in each glyph separately. Here’s a piece by Vassilis Stergioudis, it’s called ‘Wagner-Brahms’.

 

 

In this piece, the ‘W’ rotates to form a ‘B’. The ‘a’ rotates to form an ‘R’, the ‘g’ rotates to form an ‘a’ and so on.

 

I see that some letters rotate 90°, some 180° and some 270°.

 

You are absolutely right! I’m glad you noticed it. You can have any rotation that you want, but it has to take place on each glyph separately. That’s the point of rotatograms.

 

And now let’s move on to…

   Reflectograms   

 

In a reflectogram, every glyph reflects to an axis that passes through itself. Here’s a piece which is called ‘fossil record’ by Vassilis Stergioudis.

 

 

Here, every glyph reflects in a vertical axis. The ‘F’ becomes an ‘R’, the ‘O’ becomes an ‘E’ and so on.

 

But, can you have different axis of reflection in each glyph separately?

 

You nailed it! Similarly to rotatograms, a reflectogram cannot only have mirror reflections (vertical axis) like the example above, but lake reflections (horizontal axis) or diamond reflections (diagonal axis) as well. The point is that every glyph reflects to an axis that passes through itselft, no matter its direction.

 

Side note 1: A reflectogram where every glyph has a lake reflection, ends up being a lake ambigram. This happens because the placement of the letters aligns with the axis of reflection. In some sense, a lake ambigram is also a special sub-type of reflectogram.

 

Side note 2: The same happens with a reflectogram that reads vertically, when every letter is on top of the other and has mirror reflection. It ends up being a totem. This happens because the placement of the letters align with the vertical axis of reflection.

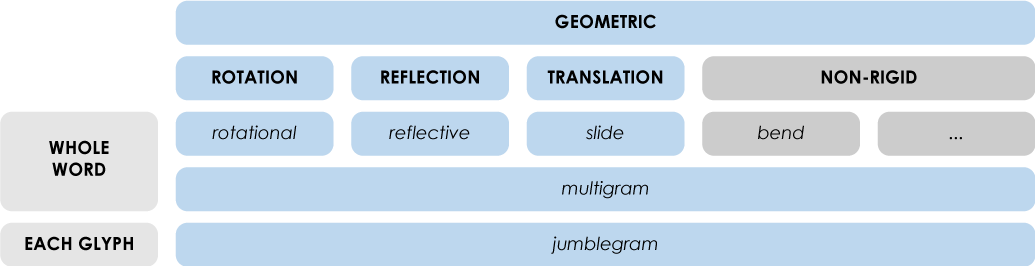
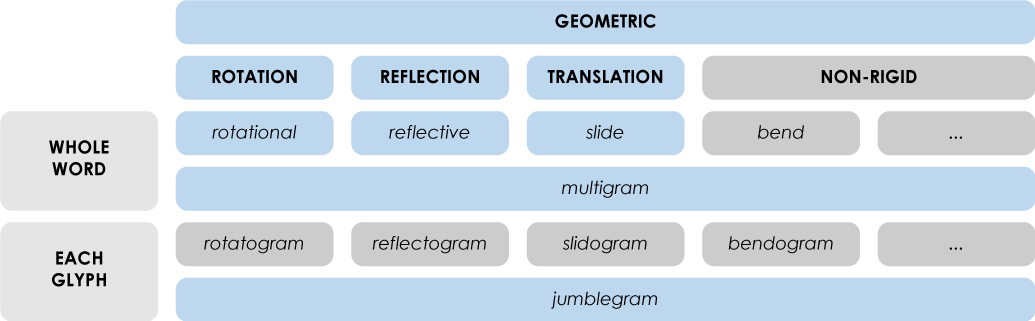
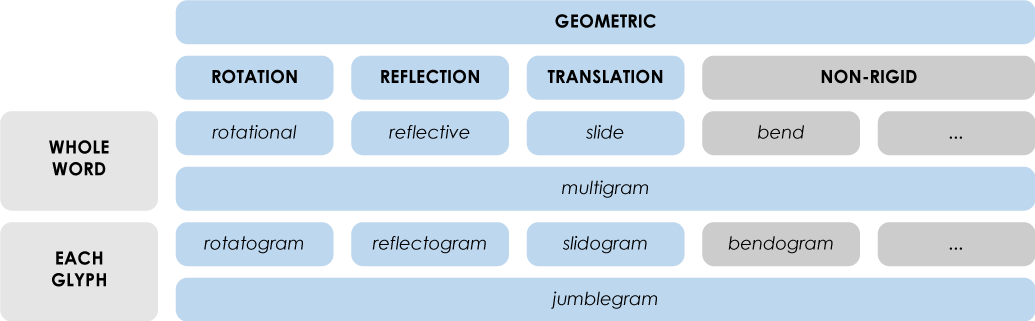
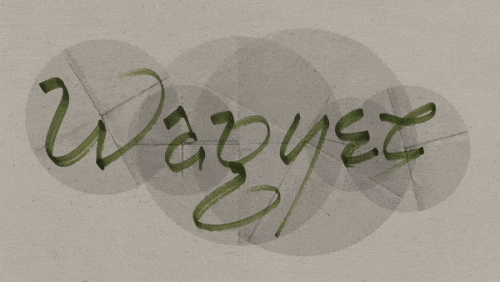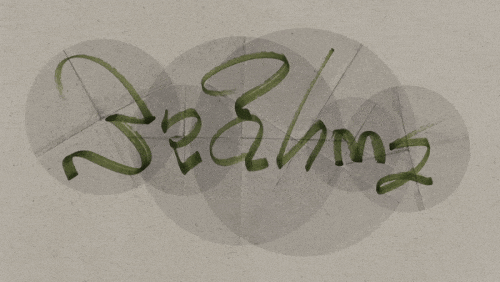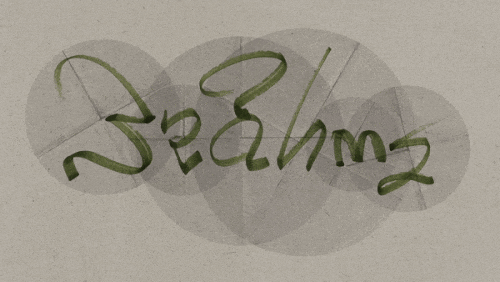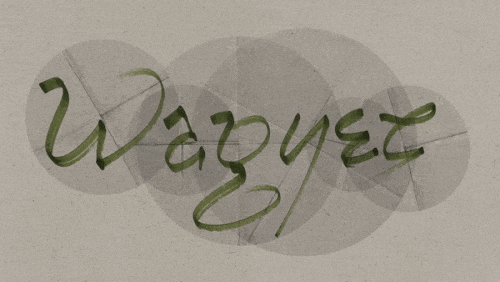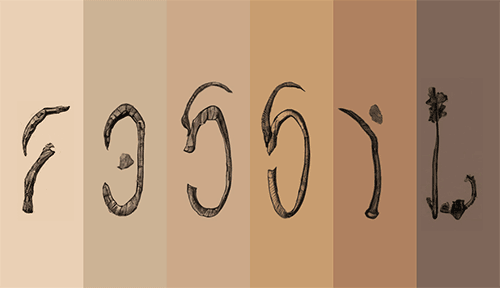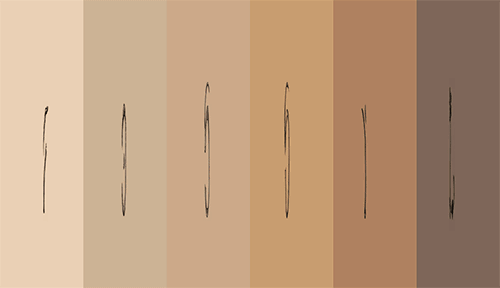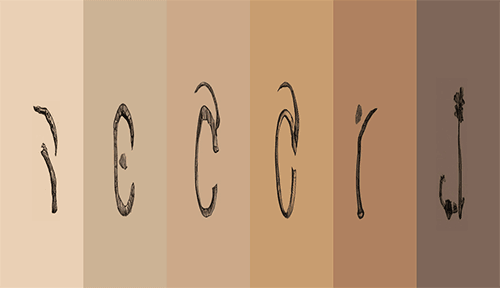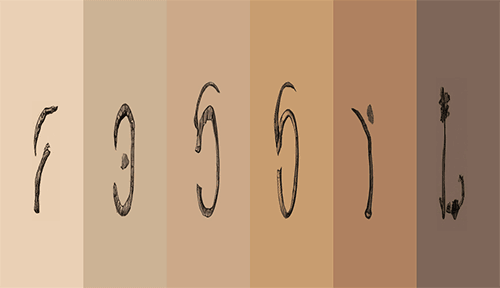   Slidograms   

 

You could call it translatogram, but I prefer slidogram. Now, can you imagine how this one would look like?

 

Hmmm… I guess that every letter would move independently?

 

That’s right! A slidogram would have each glyph move in some direction: horizontally, vertically or diagonally.

 

Here is an example. It’s the piece “Dye Key” by Vassilis Stergioudis.

 

 

Here, the D slides upward and reappears from the bottom, forming a K. The E and Y slide horizontally and change places.

 

Now let’s look at what happens when every glyph shares the same movement.

 

Side note 1: When every glyph slides vertically in the same direction, we get a vertical slidegram. This is because the vertical movement of every letter in a word results in a vertical movement of the whole word. Actually, every direction (vertically, horizontally or diagonally) applied to all letters, results in a slidegram.

 

Side note 2: When every glyph slides horizontally, with some letters moving left and some right, we get an anagram! Hooray!

 

Wait, what?

 

Yes. An anagram is a word that has it’s letters shuffled, producing a new word. Here’s the words ‘listen’ and ‘silent’.

 

 

I’ve seen anagrams but I’ve never thought they are ambigrams.

 

Well, maybe they are not so powerful, visually speaking, but they are a sub-type of slidograms. Every letter slides horizontally. So, technically, they are.

My mind hurts!

 

So does mine. But, hey! We learned something today! Let’s celebrate it. Let’s create some rotatograms, reflectograms and slidograms, my friend.

 

I’m happy too! Can you show me where we are on the geometric ambigram map?

 

Sure, here it is.

 

 

That’s nice! What’s the next step Vassilis?

 

We could stay at this geometric horizon, but I prefer we should move on to the mind one.

 

So are you saying that there is more here? Are there more geometric ambigrams?

 

Oh, absolutely my friend! But I feel that it is better for us to step back for a while, move on to the next category, where the mind plays really fascinating games, and have a thorough understanding of what an ambigram is.

 

Are you ready?

If you can’t wait the reveal of the first mind ambigram chapter, subscribe to the newsletter to be the first to find out what comes next.

 

And if you have an idea of what’s going on in the geometric horizon in the future, I’m glad to hear your thoughts. Drop a message into [email protected].